How can we predict the pH of a buffer?

Predicting the pH of a Buffer

The pH of a buffer is determined by two factors; 1) The equilibrium constant Ka of the weak acid and 2) the ratio of weak base [A^-] to weak acid [HA] in solution.

1) Different weak acids have different equilibrium constants (K_a). K_a tells us what proportion of HA will be dissociated into H⁺ and A^- in solution. The more H⁺ ions that are created, the more acidic and lower the pH of the resulting solution.

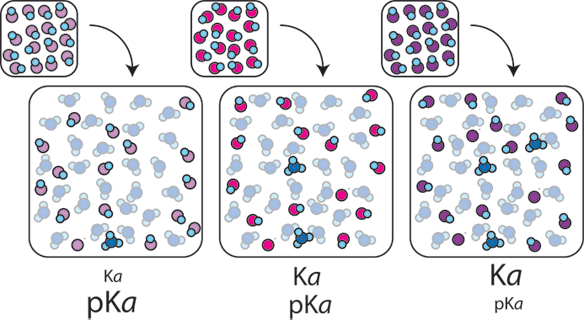
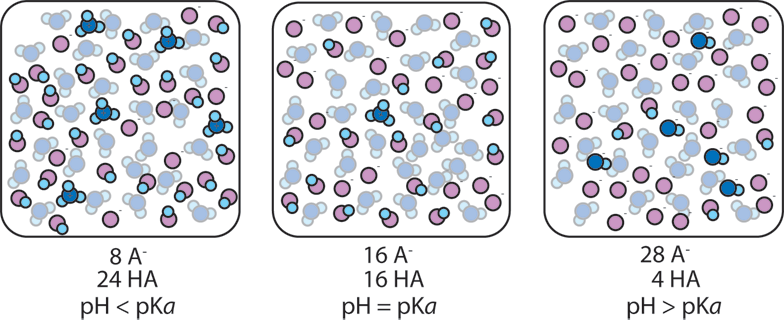
2) The ratio of A^- to HA in a buffer also affects the pH. If a buffer has more base than acid, more OH^- ions are likely to be present and the pH will rise. If a buffer has more acid than base, more H⁺ ions are present and the pH will fall. When the concentrations of A^- and HA are equal, the concentration H⁺ is equal to K_a, (or equivalently pH = pK_a).

This is formalized in the Henderson-Hasselbalch equation: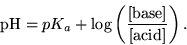

Since pK_a is a property of the weak acid we select for our buffer, we can control the pH by manipulating the proportion of weak base (A^-) and weak acid (HA) in solution.

When [A^-]/[HA] remains close to 1, the pH remains close to pK_a. As [A^-]/[HA] goes from 1/10 to 10 the pH changes from pK_a+1 to pK_a-1. So as long as [A^-]/[HA] is between 1/10 and 10, the pH is within 1 unit of pKa. The addition of a strong acid or base to a buffer changes the ratio [A^-]/[HA]. When a buffer absorbs an acid (H⁺), the acid converts A^- to HA (A^- + H⁺ → HA) and so the ratio [A^-]/[HA] decreases. When a buffer absorbs base (OH^-), the base converts HA to A^- (HA + OH^- → A^-) and so the ratio [A^-]/[HA] increases. As long as the added acid or base doesn't cause [A^-]/[HA] to go outside the range 1/10..10, the pH will remain within 1 unit of pK_a, i.e. the pH won't change by very much and the solution is therefore buffered.

See the next two pages for practice in determining the pH of a buffer solution.